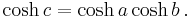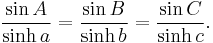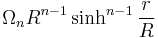Hyperbolic geometry

Lines through a given point P and asymptotic to line R.

A triangle immersed in a saddle-shape plane (a hyperbolic paraboloid), as well as two diverging ultraparallel lines.

In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai-Lobachevskian geometry) is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced. The parallel postulate in Euclidean geometry is equivalent to the statement that, in two dimensional space, for any given line l and point P not on l, there is exactly one line through P that does not intersect l; i.e., that is parallel to l. In hyperbolic geometry there are at least two distinct lines through P which do not intersect l, so the parallel postulate is false. Models have been constructed within Euclidean geometry that obey the axioms of hyperbolic geometry, thus proving that the parallel postulate is independent of the other postulates of Euclid.

Because there is no precise hyperbolic analogue to Euclidean parallel lines, the hyperbolic use of parallel and related terms varies among writers. In this article, the two limiting lines are called asymptotic and lines sharing a common perpendicular are called ultraparallel; the simple word parallel may apply to both.

A characteristic property of hyperbolic geometry is that the angles of a triangle add to less than a straight angle (half circle). In the limit as the vertices go to infinity, there are even ideal hyperbolic triangles in which all three angles are 0°.

1 Non-intersecting lines
2 Triangles
3 Circles, Spheres, and Balls
4 History
5 Models of the hyperbolic plane
6 Visualizing hyperbolic geometry
7 Homogeneous structure
8 Vectors
9 See also
10 Notes
11 References
12 External links

Non-intersecting lines

An interesting property of hyperbolic geometry follows from the occurrence of more than one parallel line through a point P: there are two classes of non-intersecting lines. Let B be the point on l such that the line PB is perpendicular to l. Consider the line x through P such that x does not intersect l, and the angle θ between PB and x counterclockwise from PB is as small as possible; i.e., any smaller angle will force the line to intersect l. This is called an asymptotic line in hyperbolic geometry. Symmetrically, the line y that forms the same angle θ between PB and itself but clockwise from PB will also be asymptotic. x and y are the only two lines asymptotic to l through P. All other lines through P not intersecting l, with angles greater than θ with PB, are called ultraparallel (or disjointly parallel) to l. Notice that since there are an infinite number of possible angles between θ and 90 degrees, and each one will determine two lines through P and disjointly parallel to l, there exist an infinite number of ultraparallel lines.

Thus we have this modified form of the parallel postulate: In hyperbolic geometry, given any line l, and point P not on l, there are exactly two lines through P which are asymptotic to l, and infinitely many lines through P ultraparallel to l.

The differences between these types of lines can also be looked at in the following way: the distance between asymptotic lines shrinks toward zero in one direction and grows without bound in the other; the distance between ultraparallel lines (eventually) increases in both directions. The ultraparallel theorem states that there is a unique line in the hyperbolic plane that is perpendicular to each of a given pair of ultraparallel lines.

In Euclidean geometry, the "angle of parallelism" is a constant; that is, any distance 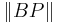$\lVert BP \rVert$ between parallel lines yields an angle of parallelism equal to 90°. In hyperbolic geometry, the angle of parallelism varies with the 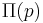$\Pi(p)$ function. This function, described by Nikolai Ivanovich Lobachevsky, produces a unique angle of parallelism for each distance $p = \lVert BP \rVert$ . 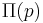As the distance gets shorter, $\Pi(p)$ approaches 90°, whereas with increasing distance 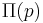$\Pi(p)$ approaches 0°. Thus, as distances get smaller, the hyperbolic plane behaves more and more like Euclidean geometry. Indeed, on small scales compared to 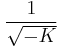$\frac{1}{\sqrt{-K}}$ , where 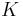$K\!$ is the (constant) Gaussian curvature of the plane, an observer would have a hard time determining whether he is in the Euclidean or the hyperbolic plane.

Triangles

Distances in the hyperbolic plane can be measured in terms of a unit of length 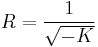$R = \frac{1}{\sqrt{-K}}$ , analogous to the radius of the sphere in spherical geometry. Using this unit of length a theorem in hyperbolic geometry can be stated which is analogous to the Pythagorean theorem. If $a, b\,$ are the legs and $c\,$ is the hypotenuse of a right triangle all measured in this unit then:

$\cosh c=\cosh a\cosh b\,.$

The cosh function is a hyperbolic function which is an analog of the standard cosine function. All six of the standard trigonometric functions have hyperbolic analogs. In trigonometric relations involving the sides and angles of a hyperbolic triangle the hyperbolic functions are applied to the sides and the standard trigonometric functions are applied to the angles. For example the law of sines for hyperbolic triangles is:

$\frac{\sin A}{\sinh a} = \frac{\sin B}{\sinh b} = \frac{\sin C}{\sinh c}.$

For more of these trigonometric relationships see hyperbolic triangles.

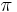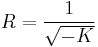Unlike Euclidean triangles whose angles always add up to 180 degrees or $\pi$ radians the sum of the angles of a hyperbolic triangle is always strictly less than 180 degrees. The difference is sometimes referred to as the defect. The area of a hyperbolic triangle is given by its defect multiplied by $R^2$ where $R = \frac{1}{\sqrt{-K}}$ . As a consequence all hyperbolic triangles have an area which is less than 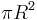$\pi{R^2}$ . The area of an ideal hyperbolic triangle is equal to this maximum.

As in spherical geometry the only similar triangles are congruent triangles.

Circles, Spheres, and Balls

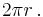In hyperbolic geometry the circumference of a circle of radius $r \,$ is greater than $2 \pi r \,.$ It is in fact equal to

$2\pi R \sinh \frac{r}{R} \,.$

Its area is

$2\pi R^2 (\cosh \frac{r}{R} - 1) \,.$

The surface area of a sphere is

$4\pi R^2 \sinh^2 \frac{r}{R} \,.$

The volume of a sphere is

$\pi R^3 \sinh \frac{2r}{R} - 2\pi R^2r \,.$

For the surface of a sphere in 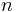$n \,$ dimensional space the corresponding expression is

$\Omega_{n} R^{n-1} \sinh^{n-1} \frac{r}{R} \,$

where the full 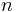$n \,$ dimensional solid angle is

$\Omega_{n}=\frac{2\pi^{n/2}}{\Gamma \left (\frac{n}{2} \right )} \,$

using $\Gamma \,$ for the Gamma function.

The volume of the ball in 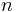$n \,$ dimensional space is:

$\Omega_{n} R^{n-1} \int_0^r \sinh^{n-1} \frac{r}{R}dr \,.$

History

A number of geometers made attempts to prove the parallel postulate by assuming its negation and trying to derive a contradiction, including Proclus, Ibn al-Haytham (Alhacen), Omar Khayyám,^[1] Nasir al-Din al-Tusi, Witelo, Gersonides, Alfonso, and later Giovanni Gerolamo Saccheri, John Wallis, Johann Heinrich Lambert, and Legendre.^[2] Their attempts failed, but their efforts gave birth to hyperbolic geometry.

The theorems of Alhacen, Khayyam and al-Tusi on quadrilaterals, including the Ibn al-Haytham–Lambert quadrilateral and Khayyam–Saccheri quadrilateral, were the first theorems on hyperbolic geometry. Their works on hyperbolic geometry had a considerable influence on its development among later European geometers, including Witelo, Gersonides, Alfonso, John Wallis and Saccheri.^[3]

In the 18th century, Johann Heinrich Lambert introduced the hyperbolic functions and computed the area of a hyperbolic triangle.

In the nineteenth century, hyperbolic geometry was extensively explored by János Bolyai and Nikolai Ivanovich Lobachevsky, after whom it sometimes is named. Lobachevsky published in 1830, while Bolyai independently discovered it and published in 1832. Carl Friedrich Gauss also studied hyperbolic geometry, describing in a 1824 letter to Taurinus that he had constructed it, but did not publish his work. In 1868, Eugenio Beltrami provided models of it, and used this to prove that hyperbolic geometry was consistent if Euclidean geometry was.

The term "hyperbolic geometry" was introduced by Felix Klein in 1871.^[4]

For more history, see article on non-Euclidean geometry, and the references Coxeter and Milnor.

Models of the hyperbolic plane

Poincaré disc model of great rhombitruncated {3,7} tiling

Lines through a given point and asymptotic to a given line, illustrated in the Poincaré disc model

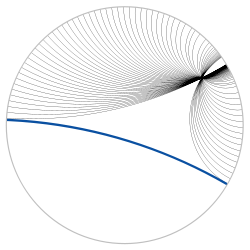
There are four models commonly used for hyperbolic geometry: the Klein model, the Poincaré disc model, the Poincaré half-plane model, and the Lorentz model, or hyperboloid model. These models define a real hyperbolic space which satisfies the axioms of a hyperbolic geometry. Despite the naming, the two disc models and the half-plane model were introduced as models of hyperbolic space by Beltrami, not by Poincaré or Klein.

The Klein model, also known as the projective disc model and Beltrami-Klein model, uses the interior of a circle for the hyperbolic plane, and chords of the circle as lines.
- This model has the advantage of simplicity, but the disadvantage that angles in the hyperbolic plane are distorted.
- The distance in this model is the cross-ratio, which was introduced by Arthur Cayley in projective geometry.
The Poincaré disc model, also known as the conformal disc model, also employs the interior of a circle, but lines are represented by arcs of circles that are orthogonal to the boundary circle, plus diameters of the boundary circle.
The Poincaré half-plane model takes one-half of the Euclidean plane, as determined by a Euclidean line B, to be the hyperbolic plane (B itself is not included).
- Hyperbolic lines are then either half-circles orthogonal to B or rays perpendicular to B.
- Both Poincaré models preserve hyperbolic angles, and are thereby conformal. All isometries within these models are therefore Möbius transformations.
- The half-plane model is identical (at the limit) to the Poincaré disc model at the edge of the disc
The Lorentz model or hyperboloid model employs a 2-dimensional hyperboloid of revolution (of two sheets, but using one) embedded in 3-dimensional Minkowski space. This model is generally credited to Poincaré, but Reynolds (see below) says that Wilhelm Killing and Karl Weierstrass used this model from 1872.
- This model has direct application to special relativity, as Minkowski 3-space is a model for spacetime, suppressing one spatial dimension. One can take the hyperboloid to represent the events that various moving observers, radiating outward in a spatial plane from a single point, will reach in a fixed proper time. The hyperbolic distance between two points on the hyperboloid can then be identified with the relative rapidity between the two corresponding observers.

Visualizing hyperbolic geometry

Circle Limit III, 1959

A collection of crocheted hyperbolic planes, in imitation of a coral reef, by the Institute For Figuring

A coral with similar geometry on the Great Barrier Reef

M. C. Escher's famous prints Circle Limit III and Circle Limit IV illustrate the conformal disc model quite well. The white lines in III are not quite geodesics (they are hypercycles), but are quite close to them. It is also possible to see quite plainly the negative curvature of the hyperbolic plane, through its effect on the sum of angles in triangles and squares.

For example, in Circle Limit III every vertex belongs to three triangles and three squares. In the Euclidean plane, their angles would sum to 450°; i.e., a circle and a quarter. From this we see that the sum of angles of a triangle in the hyperbolic plane must be smaller than 180°. Another visible property is exponential growth. In Circle Limit III, for example, one can see that the number of fishes within a distance of n from the center rises exponentially. The fishes have equal hyperbolic area, so the area of a ball of radius n must rise exponentially in n.

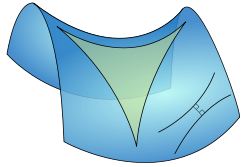
There are several ways to physically realize a hyperbolic plane (or approximation thereof). A particularly well-known paper model based on the pseudosphere is due to William Thurston. The art of crochet has been used to demonstrate hyperbolic planes with the first being made by Daina Taimina^[5], whose book Crocheting Adventures with Hyperbolic Planes won the 2009 Bookseller/Diagram Prize for Oddest Title of the Year.^[6] In 2000, Keith Henderson demonstrated a quick-to-make paper model dubbed the "hyperbolic soccerball".

Homogeneous structure

Hyperbolic space of dimension n is a special case of a Riemannian symmetric space of noncompact type, as it is isomorphic to the quotient

$O(1,n)/(O(1) \times O(n))$ .

The orthogonal group O(1,n) acts by norm-preserving transformations on Minkowski space 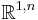$\mathbb{R}^{1,n}$ , and it acts transitively on the two-sheet hyperboloid of norm 1 vectors. Timelike lines (i.e., those with positive-norm tangents) through the origin pass through antipodal points in the hyperboloid, so the space of such lines yields a model of hyperbolic n-space. The stabilizer of any particular line is isomorphic to the product of the orthogonal groups O(n) and O(1), where O(n) acts on the tangent space of a point in the hyperboloid, and O(1) reflects the line through the origin. Many of the elementary concepts in hyperbolic geometry can be described in linear algebraic terms: geodesic paths are described by intersections with planes through the origin, dihedral angles between hyperplanes can be described by inner products of normal vectors, and hyperbolic reflection groups can be given explicit matrix realizations.

In small dimensions, there are exceptional isomorphisms of Lie groups that yield additional ways to consider symmetries of hyperbolic spaces. For example, in dimension 2, the isomorphisms 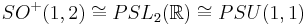$SO^+(1,2) \cong PSL_2(\mathbb{R}) \cong PSU(1,1)$ allow one to interpret the upper half plane model as the quotient 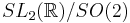$SL_2(\mathbb{R})/SO(2)$ and the Poincaré disc model as the quotient $SU(1,1)/U(1)$ . 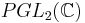In both cases, the symmetry groups act by fractional linear transformations, since both groups are the orientation-preserving stabilizers in $PGL_2(\mathbb{C})$ of the respective subspaces of the Riemann sphere. The Cayley transformation not only takes one model of the hyperbolic plane to the other, but realizes the isomorphism of symmetry groups as conjugation in a larger group. In dimension 3, the fractional linear action of 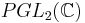$PGL_2(\mathbb{C})$ on the Riemann sphere is identified with the action on the conformal boundary of hyperbolic 3-space induced by the isomorphism 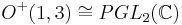$O^+(1,3) \cong PGL_2(\mathbb{C})$ . This allows one to study isometries of hyperbolic 3-space by considering spectral properties of representative complex matrices. For example, parabolic transformations are conjugate to rigid translations in the upper half-space model, and they are exactly those transformations that can be represented by unipotent upper triangular matrices.

Vectors

The difference between hyperbolic vectors and euclidean vectors is that addition of vectors in hyperbolic geometry is nonassociative and noncommutative. However this doesn't mean that A+(B+C) & (A+B)+C and A+B & B+A are totally unrelated. The exact relations are given by gyroassociativity and gyrocommutativity laws.

Notes

↑ See for instance, "Omar Khayyam 1048-1131". http://www.resonancepub.com/omarkhayyam.htm. Retrieved 2008-01-05.
↑ http://www.math.columbia.edu/~pinkham/teaching/seminars/NonEuclidean.html
↑ Boris A. Rosenfeld and Adolf P. Youschkevitch (1996), "Geometry", in Roshdi Rashed, ed., Encyclopedia of the History of Arabic Science, Vol. 2, p. 447-494 [470], Routledge, London and New York:

"Three scientists, Ibn al-Haytham, Khayyam and al-Tusi, had made the most considerable contribution to this branch of geometry whose importance came to be completely recognized only in the nineteenth century. In essence their propositions concerning the properties of quadrangles which they considered assuming that some of the angles of these figures were acute of obtuse, embodied the first few theorems of the hyperbolic and the elliptic geometries. Their other proposals showed that various geometric statements were equivalent to the Euclidean postulate V. It is extremely important that these scholars established the mutual connection between this postulate and the sum of the angles of a triangle and a quadrangle. By their works on the theory of parallel lines Arab mathematicians directly influenced the relevant investigations of their European counterparts. The first European attempt to prove the postulate on parallel lines - made by Witelo, the Polish scientists of the thirteenth century, while revising Ibn al-Haytham's Book of Optics (Kitab al-Manazir) - was undoubtedly prompted by Arabic sources. The proofs put forward in the fourteenth century by the Jewish scholar Levi ben Gerson, who lived in southern France, and by the above-mentioned Alfonso from Spain directly border on Ibn al-Haytham's demonstration. Above, we have demonstrated that Pseudo-Tusi's Exposition of Euclid had stimulated both J. Wallis's and G. Saccheri's studies of the theory of parallel lines."
↑ F. Klein, Über die sogenannte Nicht-Euklidische, Geometrie, Math. Ann. 4, 573-625 (cf. Ges. Math. Abh. 1, 244-350).
↑ "Hyperbolic Space". The Institute for Figuring. December 21, 2006. http://theiff.org/oexhibits/oe1e.html. Retrieved January 15, 2007.
↑ Bloxham, Andy (March 26, 2010). "Crocheting Adventures with Hyperbolic Planes wins oddest book title award". The Telegraph. http://www.telegraph.co.uk/culture/books/bookprizes/7520047/Crocheting-Adventures-with-Hyperbolic-Planes-wins-oddest-book-title-award.html .

References

Coxeter, H. S. M., (1942) Non-Euclidean geometry, University of Toronto Press, Toronto
Fenchel, Werner (1989). Elementary geometry in hyperbolic space. De Gruyter Studies in mathematics. 11. Berlin-New York: Walter de Gruyter & Co..
Fenchel, Werner; Nielsen, Jakob; edited by Asmus L. Schmidt (2003). Discontinuous groups of isometries in the hyperbolic plane. De Gruyter Studies in mathematics. 29. Berlin: Walter de Gruyter & Co..
Milnor, John W., (1982) Hyperbolic geometry: The first 150 years, Bull. Amer. Math. Soc. (N.S.) Volume 6, Number 1, pp. 9–24.
Reynolds, William F., (1993) Hyperbolic Geometry on a Hyperboloid, American Mathematical Monthly 100:442-455.
Stillwell, John., (1996) Sources in Hyperbolic Geometry, volume 10 in AMS/LMS series History of Mathematics.
Samuels, David., (March 2006) Knit Theory Discover Magazine, volume 27, Number 3.
James W. Anderson, Hyperbolic Geometry, Springer 2005, ISBN 1-85233-934-9
James W. Cannon,, William J. Floyd, Richard Kenyon, and Walter R. Parry (1997) Hyperbolic Geometry, MSRI Publications, volume 31.

External links

Visions of Infinity: Tiling a hyperbolic floor inspires both mathematics and art Science News: Dec. 23, 2000; Vol. 158, No. 26/27, p. 408
Java freeware for creating sketches in both the Poincaré Disk and the Upper Half-Plane Models of Hyperbolic Geometry University of New Mexico
"The Hyperbolic Geometry Song" A short music video about the basics of Hyperbolic Geometry available at Youtube.
Weisstein, Eric W., "Gauss-Bolyai-Lobachevsky Space" from MathWorld.
Weisstein, Eric W., "Hyperbolic Geometry" from MathWorld.
More on hyperbolic geometry, including movies and equations for conversion between the different models University of Illinois at Urbana-Champaign
Stothers, Wilson (2000). Hyperbolic geometry. University of Glasgow. http://www.maths.gla.ac.uk/~wws/cabripages/hyperbolic/hyperbolic0.html , interactive instructional website.